Overview
One topic I love to talk about is an algorithm for building random dungeons. A dungeon is essentially a maze which could be one of many styles. The style of dungeons that I enjoy is one where there are connected rooms, and one must crawl their way through the dungeon in search of something, perhaps an exit.The Binary Space Partitioning (BSP) algorithm is a very interesting one, because it provides an absolutely wonderful way of building a random dungeon in the style that I enjoy. When combined with dungeon generation, it can develop truly fantastic procedural content generation (PCG). Behold:
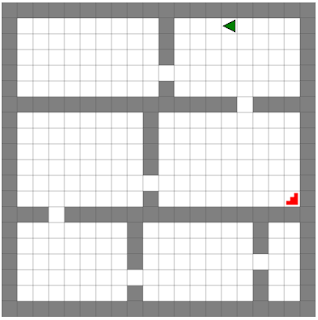 |
| A random dungeon built using the BSP algorithm. The green triangle is the player and the red stairs represent an exit. |
The fully connected property is very cool in PCG. It prevents the need to perform content validation, meaning the complexity for this kind of dungeon generation is efficient, whereas this is sometimes a drawback to deploying PCG solutions in gaming.
Details
As a recursive algorithm, this kind of dungeon generation is difficult to analyze. It works by roughly splitting the area until the rooms are small enough, but it also does so in a random manner. Consider the starting point, which is a dungeon with no interior walls and only an exterior outside boundary wall: |
| An empty dungeon with only the player and an exit. |
The first step of our algorithm is to then choose randomly to either split this in half vertically or horizontally. Running this with a fixed random seed, I can pause the algorithm and tell it when to stop, allowing me to generate these pictures. We can see that in the first division, the algorithm chose to split horizontally.
 |
| A single partition has generated a dungeon having two rooms. |
In choosing to split horizontally, the algorithm chose a semi-random location to do so; somewhere near the middle, for aesthetic purposes, and not riding along the edges of the outer dungeon. After adding the wall for the split, the next step was to provide an entryway to reach from one side to the other. This is what allows for the fully connected property.
Going one step further, the algorithm will traverse into both of the newly created halves.
 |
| An addition split in the northern room now produces a three-room dungeon. |
 |
| Four-room dungeon with yet another partition. |
Continuing into the top-most of the new partitions, a split was chosen vertically. The entryway was placed, and recursion continues into both of the new partitions. Only this time, since the (top left) room was considered sufficiently small enough (termination criteria of the recursion), it stopped subdividing and moves onto the next sibling (top right room).
The same situation happens in that room as well, and so the traversal visits the next sibling, which is the middle room. The middle is fortunately wide enough to split vertically, although not tall enough to split horizontally, so the choice is forced to be a vertical split.
 |
| Five-room dungeon. |
And so on. These middle rooms are small enough. Hence, we move onto the bottom room which again can only be split vertically, giving us our final result as that split produces sufficiently small rooms.
In each of these partitions, care is given not to select a split that might potentially obscure a previously installed entryway.
The BSP algorithm also has a by-product, called the BSP-Tree, which is easy to see. The root node is the empty room, and a single split divides the tree into two. It is always a binary tree and it is with this tree we can prove that the dungeon is fully connected.
Conclusion
There are many applications of the BSP algorithm, but creating dungeons with it is one of my favorite. Hopefully this blog post will have enlightened a game developer and inspired ideas. In the future, I will drop some code onto this post and detail how it works to implement this kind of random dungeon generation.